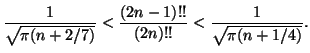Abstracts

  1. We consider a class of algebraic inequalities for functions of n variables depending on parameters that generalise the case of GA-convex functions. The functions in this class are GA-convex only in a subdomain of definition yet the inequality for GA-convexity still holds on the whole domain if suitable conditions are satisfied by the parameters. The method is elementary and allows us to give further extensions to a large class of functions. 
    As an application we show the validity of an n-dimensional generalization of a conjectured inequality related to a problem given at the 42nd IMO held at Washington DC (USA) in 2001. 

  2. By mathematical induction, an identity and a double inequality for remainder of power series of tangent function are established.

  3. An approximation of the Fourier Sine Transform via Grüss, Chebychev and Lupas integral inequalities and application for an electrical curcuit containing an inductance L, a condenser of capacity C and a source of electromotive force E0 P(t) , where P(t) is an L2-integrable function, are given.

  4. In this paper, the concepts of Euler numbers and Euler polynomials are generalized, and some basic properties are investigated.

  5. Using some techniques developed by Dragomir and Wang in the recent paper [2] in connection to Ostrowski integral inequality, we point out some approximation results for the Henkel's transform of absolutely continuous mapping.

  6.  We consider a family of two-point quadrature formulae and establish sharp estimates for the remainders under various regularity conditions. Improved forms of certain integral inequalities due to Hermite-Hadamard, Iyengar, Milovanovic-Pecaric, and others are obtained as special cases. Our results can also be interpreted as analogues to a theorem of Ostrowski on the deviation of a function from its averages. Furthermore, we establish a generalization of
    a result of Fink concerning Lp estimates for the remainder of the trapezoidal rule and present the best constants in the error bounds.

  7.  Hadamard-type inequalities are derived for g-convex dominated maps. Applications are given involving two functionals and some common means.

 

  1. Some maps are defined which derive naturally from weighted geometric means. They are shown to have convenient monotonicity and supermultiplicativity properties.

  2. In this paper improvements of the Ostrowski and generalised Trapezoid inequalities are found in terms of the upper and lower bounds of the first derivative.

  3. By the use of the Cauchy mean value theorem, some new inequalities of Ostrowski type are given.

  4. An inequality for a normalised isotonic linear functional of Grüss type and particular cases for integrals and norms are established. Applications in obtaining a counterpart for the Cauchy-Buniakowski-Schwartz inequality for functionals and Jessen's inequality for convex functions are also given.

  5. A companion of the Grüss inequality in the general setting of measurable spaces and abstract Lebesgue integrals is proven. Some particular inequalities are mentioned as well. An application for the moments of guessing mapping is also provided.

  6. New bounds are developed for the Cebyšev functional utilising an identity involving a Riemann-Stieltjes integral. A refinement of the classical Cebyšev inequality is produced for $f$ monotonic non-decreasing, $g$ continuous and $\mathcal{M}\left( g;t,b\right) -\mathcal{%% M}\left( g;a,t\right) \geq 0,$ for $t\in \left[ a,b\right] $ where $\mathcal{%% M}\left( g;c,d\right) $ is the integral mean over $\left[ c,d\right] .$

     

  7.   A Grüss related integral inequality in the general setting of measurable spaces and abstract Lebesgue integrals is proven. Some particular inequalities and applications for Ostrowski and generalized Trapezoid inequality are mentioned as well.
         

  8. The function $ f(x)=\frac{[\Gamma(x+1)]^{1/x}}{x+1}$ is strictly decreasing on $ [1,\infty)$, the function $ g(x)=\frac{[\Gamma(x+1)]^{1/x}}{\sqrt{x}}$ is strictly increasing on $ [2,\infty)$, and the function $ h(x)=\frac{[\Gamma(x+1)]^{1/x}}{\sqrt{x+1}}$ is strictly increasing on $ [1,\infty)$, respectively. From these, some inequalities, for example, the Minc-Sathre inequality, are deduced, and two open problems posed by the second author are partially solved.

     

  9. The "Median Principle" for different integral inequalities of Grüss and Ostrowski type is applied.

  10. A generalised integration by parts formula for sequences of absolutely continuous functions that satisfy the w-Appell condition and different estimates for the remainder are provided. Applications for particular instances of such sequences are pointed out as well.

  11. Some inequalities for the Hilbert transform of the product of two functions are given.

  12. The properties of some sequences of functions defined by multiple integrals associated with the Hermite-Hadamard integral inequality for convex functions are studied.

  13. Some inequalities and approximations for the finite Hilbert transform by the use of Ostrowski type inequalities for absolutely continuous functions are given.

  14. In this paper an inequality of Ostrowski type in terms of the lower and upper bounds of the first derivative is found.

  15. For all natural number $ n$, we have
    $\displaystyle \frac1{\sqrt{\pi(n+2/7)}}<\frac{(2n-1)!!}{(2n)!!}<\frac1{\sqrt{\pi(n+1/4)}}.$    
    The constants $ \frac27$ and $ \frac14$ are the best possible. From this, the well-known Wallis' inequality is improved.

     

  16. A generalized f-divergence for probability vectors and some fundamental inequalities are pointed out.

  17. In this paper we introduce the concepts of p-logarithmic and a power divergence measures and point out a number of basic results.

  18. Sharp bounds of the Cebysev functional for the Stieltjes integrals similar to the Grüss one and applications for quadrature rules are given.

  19. In this paper, some new estimates of the Cebysev functional considered in [1] are provided. Applications for quadrature formulae in approximating the Riemann-Stieltjes integral are also given.

  20. A companion of Ostrowski's inequality for functions of bounded variation and applications are given.

  21. Companions of Ostrowski's integral ineqaulity for absolutely continuous functions and applications for composite quadrature rules and for p.d.f.'s are provided.

  22. An Ostrowski type inequality for absolutely continuous functions whose derivatives are convex and applications are given.

  23. Some inequalities and approximations for the finite Hilbert transform by the use of Taylor's formula with the integral remainder are given.

  1. An approximation for the Fourier transforms of absolutely continuous mappings in terms of the exponential mean, and the study of error bounds when g' Î Lp[a,b] (1£p£¥) are given.