-
An inequality of the Lupas type for
Cebysev functionals is established.
-
Some sums of series of Rogers dilogarithm functions are established by Abel's functional equation.
-
In this article, for
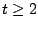 , a general generalization of Jordan's
inequality
, a general generalization of Jordan's
inequality
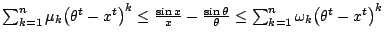 for
for
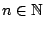 and
and
![$\theta\in(0,\pi]$](abstracts/jordan-generalized_ab/img4.gif) is established, where
the coefficients
is established, where
the coefficients 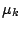 and
and 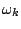 defined by recursing
formulas (11) and (12) are the best possible. As an application,
L. Yang's inequality is refined.
defined by recursing
formulas (11) and (12) are the best possible. As an application,
L. Yang's inequality is refined.
-
In this short paper, it is proved that the function
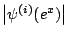 for
for
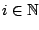 is subadditive in
is subadditive in
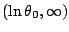 and superadditive in
and superadditive in
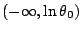 , where
, where
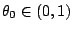 is the unique
root of equation
is the unique
root of equation
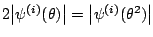 .
.
-
In this article, van der Corput's inequality is generalized by using the well
known Euler-Maclaurin sum formula and other analytic techniques.
-
Sharp error estimates in approximating the Stieltjes integral with bounded
integrands and bounded integrators respectively, are given. Applications for
three point quadrature rules of n-time differentiable functions are also
provided.
-
An approximation of the Stieltjes integral of bounded integrals and
continuous integrators via the Darst-Pollard inequality is given. Applications for the generalised trapezoid formula and the Ostrowski
inequality for functions of bounded variation are also provided.
-
Some inequalities related to the Hölder integral inequality and
applications for bounding the Cebysev functional are given.
-
An iterative approach is used to represent multidimensional integrals in
terms of lower dimensional integrals and function evaluations. The procedure
is quite general utilising one dimensional identities as the generator
to procure multidimensional identities. Bounds are obtained from the identities. Both weighted and unweighted integrals are considered.
-
Upper and lower bounds for the norm of a linear combination of vectors are
given. Applications in obtaining various inequalities for the quantities
|| x/||x|| -y||y|| || and || x/||y||
-y||x|| || , where x and y are nonzero vectors, that are
related to the Massera-Schäffer and the Dunkl-Williams inequalities are also
provided. Some bounds for the unweighted Cebysev functional are given as well.
-
New upper and lower bounds for the p-angular distance
in normed linear spaces are given. Some of the obtained upper bounds are better than
the corresponding results due to L. Maligranda recently established in the paper [Simple norm inequalities,
Amer. Math. Monthly, 113 (2006), 256-260].
-
In this paper, we introduce 3-dimensional
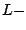 summing method,
which is a rearrangement of the summation
summing method,
which is a rearrangement of the summation 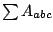 with
with
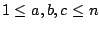 . Applying this method on some special arrays,
we obtain some identities on the Riemann zeta function and digamma
function. Also, we give a Maple program for this method to obtain
identities with input various arrays and out put identities
concerning some elementary functions and hypergeometric functions.
Finally, we introduce a further generalization of
. Applying this method on some special arrays,
we obtain some identities on the Riemann zeta function and digamma
function. Also, we give a Maple program for this method to obtain
identities with input various arrays and out put identities
concerning some elementary functions and hypergeometric functions.
Finally, we introduce a further generalization of 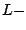 summing
method in higher dimension spaces.
summing
method in higher dimension spaces.
-
Some inequalities in normed algebras that provides lower and upper bounds
for the norm of
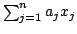 are obtained. Applications for
estimating the quantities
are obtained. Applications for
estimating the quantities
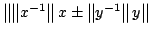 and
and
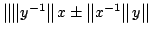 for
invertible elements
for
invertible elements 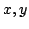 in unital normed algebras are also given.
in unital normed algebras are also given.
-
An operator
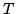 is called
is called
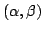 -normal
-normal
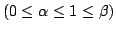 if
if
In this paper, we establish various inequalities between the operator norm
and its numerical radius of
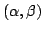 -normal operators in Hilbert
spaces. For this purpose, we employ some classical inequalities for vectors
in inner product spaces.
-normal operators in Hilbert
spaces. For this purpose, we employ some classical inequalities for vectors
in inner product spaces.
-
A refinement of the discrete Jensen's inequality for convex functions
defined on a convex subset in linear spaces is given. Application for f-divergence measures including the Kullback-Leibler and Jeffreys divergences
are provided as well.
-
A new sharp bound of the Cebysev functional for the
Riemann-Stieltjes integral is obtained. Applications for quadrature rules including the trapezoid and mid-point rule are given.
-
Sharp bounds for the deviation of a real-valued function
f defined on a compact interval [a,b] to the chord generated by its end
points (a, f(a)) and (b, f(b))
under various assumptions for f and f' including absolute continuity, convexity, bounded variation, monotonicity etc., are
given. Some applications for weighted means and f-divergence measures in
Information Theory are also provided.
-
Some new sharp upper bounds for the absolute value of the error functional
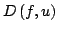 in approximating the Riemann-Stieltjes integral
in approximating the Riemann-Stieltjes integral
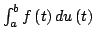 by the quantity
by the quantity
![$ \left[
u\left( b\right) -u\left( a\right) \right] \cdot \frac{1}{b-a}
\int_{a}^{b}f\left( t\right) dt$](abstracts/ARSICTF_ab/img3.gif) are given.
are given.