On the Comparison of Cauchy Mean Values
László Losonczi
Suppose that
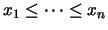 and
and
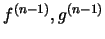 exist, with
exist, with
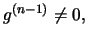 on
on ![$ [x_1,x_n]$](img4.gif) . Then there is a
. Then there is a
![$ t\in [x_1,x_n] $](img5.gif) (moreover
(moreover
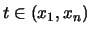 if
if
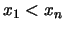 ) such that
) such that
where
![$ [x_1,\dots,x_n]_f$](img9.gif) denotes the divided difference of
denotes the divided difference of 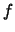 at
the points
at
the points
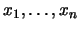 . This is the Cauchy Mean Value Theorem
for divided differences (see e.g. E. Leach and M. Sholander, Multi-variable extended mean values, J. Math. Anal. Appl., 104 1984, 390-407).
. This is the Cauchy Mean Value Theorem
for divided differences (see e.g. E. Leach and M. Sholander, Multi-variable extended mean values, J. Math. Anal. Appl., 104 1984, 390-407).
If the function
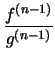 is invertible then
is invertible then
is a mean value of
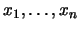 . It is called the Cauchy
mean of the numbers
. It is called the Cauchy
mean of the numbers
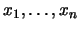 and will be denoted by
and will be denoted by
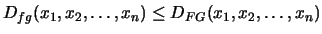 .
.
Here we completely solve the comparison problem of Cauchy means
where
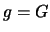 is fixed, in the special
cases
is fixed, in the special
cases 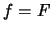 ,
, 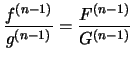 and
and
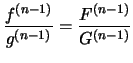 .
In the general case we find necessary conditions (which are not
sufficient) and also sufficient conditions (which are not
necessary).
.
In the general case we find necessary conditions (which are not
sufficient) and also sufficient conditions (which are not
necessary).
![]() and
and
![]() exist, with
exist, with
![]() on
on ![]() . Then there is a
. Then there is a
![]() (moreover
(moreover
![]() if
if
![]() ) such that
) such that
![$\displaystyle \displaystyle{\frac{[x_1,\dots,x_n]_f}{[x_1,\dots,x_n]_g}}=\displaystyle{\frac{f^{(n-1)}(t)}{g^{(n-1)}(t) }}
$](img8.gif)
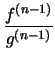 is invertible then
is invertible then
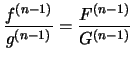 and
and
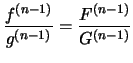 .
In the general case we find necessary conditions (which are not
sufficient) and also sufficient conditions (which are not
necessary).
.
In the general case we find necessary conditions (which are not
sufficient) and also sufficient conditions (which are not
necessary).