The Maximal Order of a Class of Multiplicative Arithmetical Functions

L´ASZLó T´OTH
University of Pécs,
Institute of Mathematics and Informatics,
Hungary, 7624 Pécs, Ifjúság u.6,

Abstract:

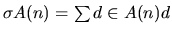
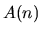
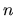
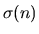
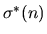
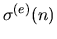
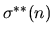
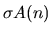
We give the maximal order of a class of multiplicative arithmetical functions, including certain functions of the type $\sigma A(n)= \sum {d \in A(n)} d$, where $A(n)$ is a subset of the set of all positive divisors of $n$. 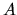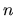As special cases we obtain the maximal orders of the divisor-sum function $\sigma(n)$ and its analogues $\sigma^*(n)$, $\sigma^{(e)} (n)$, $\sigma^{**} (n)$, $\sigma A(n)$, representing the sum of unitary divisors, exponential divisors, bi-unitary divisors and elements of a regular system $A$ of divisors of $n$, respectively. 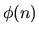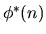We also give the minimal order of another class of multiplicative functions, including the Euler function $\phi(n)$, its unitary analogue $\phi^*(n)$ and their common generalizations. 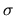We pose the problem of finding the maximal order of a $\sigma$-type function not covered by our results.