A Geometric Mean in the Furuta Inequality

Masatoshi Fujii
Osaka Education University, Japan

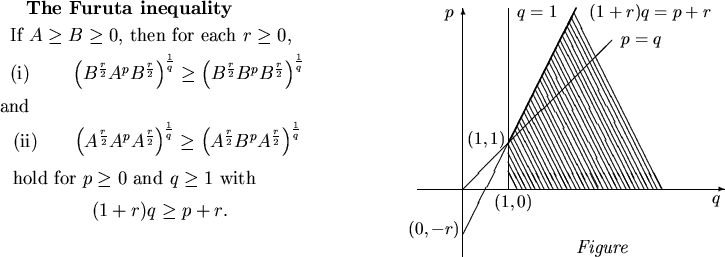
First of all, we cite the Furuta inequality [3]:

 

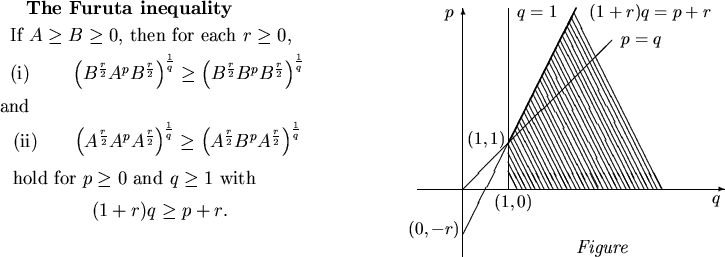
\begin{figure} % latex2html id marker 64 \setlength{\unitlength}{1mm}{\small \be... ...,-2){19.5}} \put(45,6){{\normalsize {\em Figure}}} \end{picture} } \end{figure}

Afterwards, Ando [1] proposed a variant of the Furuta inequality, which is extended to a two variable version as follows:

For $A, B > 0$, $A \gg B$, i.e., $\log A \ge \log B$, if and only if

\begin{displaymath} \left( A^{\frac{r}{2}}A^pA^{\frac{r}{2}} \right)^{\frac{r}{p... ...left( A^{\frac{r}{2}}B^pA^{\frac{r}{2}} \right)^{\frac{r}{p+r}}\end{displaymath}
It is represented in terms of the monotonicity of an operator function in the following way, [2]
   
Theorem A   For $A, B > 0$, $A \gg B$ if and only if for each $s \ge 0$, $F(t,r)= A^{-r} \sharp_{\frac{s+r}{t+r}} B^t$ is an increasing function of both $t \ge s$ and $r \ge 0$, where $\sharp_{\alpha}$ is the $\alpha$-geometric mean.

Recently Uchiyama [5] discussed some extensions of the Furuta inequality by using the operator means established by Kubo-Ando. For this, he paid his attention to the Jensen inequality for operator concave functions.

Theorem B   If $A \le B !_\mu C$ for $A,B,C > 0$, then
\begin{displaymath}B^s  \nabla_\mu C^s \le A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  \nabla_\mu C^t) \end{displaymath}
for $r \ge 0$ and $t \ge s \ge 0$, where $!_\mu$ and $\nabla_\mu$ are $\mu$-harmonic and arithmetic means respectively.

Very recently, we found the following result in [4] which is based on Theorem A.

Theorem C   Suppose that $A,B,C > 0$ and $r, s \ge 0$. If $A^t \ll B^t \nabla_\mu C^t$ for all $t \ge 0$, then
\begin{displaymath}f(t) = A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  \nabla_\mu C^t)\end{displaymath}
is an increasing function of $t \ge s$. On the other hand, if $A^t \ll B^t !_\mu C^t$ for all $t \ge 0$, then
\begin{displaymath}h(t) = A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  !_\mu C^t)\end{displaymath}
is a decreasing function of $t \ge s$.

In this talk, we discuss Theorem C and related inequalities. We begin with the following lemma.
  

Lemma 1   For $B,C>0$ and $\mu \in [0,1]$, $\log (B^t \nabla_\mu C^t)^{1/t}$ converges to $\mu \log B + (1-\mu) \log C$ decreasingly as $t \searrow 0$. Consequently there exists
\begin{displaymath}s-\lim (B^t \nabla_\mu C^t)^{1/t} = e^{\mu \log B + (1-\mu) \log C}. \end{displaymath}
 
Definition 1   For $B,C>0$ and $\mu \in [0,1]$,
\begin{displaymath}B \diamondsuit _\mu  C = e^{\mu\log B +(1-\mu)\log C} \end{displaymath}
is said to be the $\mu$-chaotically geometric mean of $B$ and $C$.

Theorem 2   For $B,C>0$ and $\mu \in [0,1]$, the following statements are mutually equivalent:

(1) $A \ll B \diamondsuit _\mu  C$.

(2) $ B^s  \nabla_\mu C^s \le A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  \nabla_\mu C^t) $ for $r \ge 0$ and $t \ge s \ge 0$.

(3) For each $r, s \ge 0$, $ f(t) = A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  \nabla_\mu C^t)$ is an increasing function of $t \ge s$.

Related to Theorem B, we have the following results.

Theorem 3   Suppose that $A,B,C > 0$ satisfy $A \ll (B^{t_0} \nabla_\mu C^{t_0})^{1/t_0}$ for some $t_0$. If $t_0 \ge 0$, then
\begin{displaymath}B^s  \nabla_\mu C^s \le A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  \nabla_\mu C^t) \end{displaymath}
 
for all $r \ge 0$ and $t \ge s \ge 0$ with $t \ge t_0$. On the other hand, if $t_0 < 0$, then
\begin{displaymath}(B^t  !_\mu C^t)^{\frac{s}{t}} \le A^{-r} \sharp_{\frac{s+r}{t+r}} (B^t  !_\mu C^t) \end{displaymath}
 

for all $r \ge 0$ and $-t_0 \ge t \ge s \ge 0$.