


Next: About this document ...
Up: A geometric mean in
Previous: A geometric mean in
- 1
-
T.ANDO,
On some operator inequalities,
Math. Ann., 279(1987), 157-159.
- 2
-
M.FUJII, T.FURUTA AND E.KAMEI,
Furuta's inequality and application to Ando's theorem,
Linear Alg. and Appl., 179(1993), 161-169.
- 3
-
T. FURUTA,
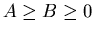 assures
assures
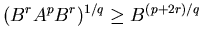 for
for
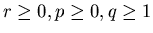 with
with
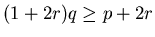 ,
Proc. Amer. Math. Soc., 101(1987), 85-88.
,
Proc. Amer. Math. Soc., 101(1987), 85-88.
- 4
-
T. FURUTA AND E. KAMEI,
An extension of Uchiyama's result associated with an order preserving operator inequality,
preprint.
- 5
-
E. KAMEI,
A satellite to Furuta's inequality,
Math. Japon., 33(1988), 883-886.
- 6
-
M. UCHIYAMA,
An operator inequality related to Jensen's inequality,
preprint.
Pui Ling Pang
2001-04-20